Quantum Light
Light is normally thought of as an electromagnetic wave at optical frequencies. What we call light can reasonably be extended to the near infrared and ultraviolet parts of the spectrum, all of which satisfy Maxwell’s equations for the electromagnetic field. We can use these to write down a wave equation for the electric and magnetic fields whose solution is waves which travel at speed c – the speed of light and one of the fundamental constants of the universe. These waves are harmonic – they satisfy the simple harmonic oscillator equation and this gives a clue to the next part of the story.
We know that the world is not classical. At some fundamental level quantum graininess must appear. We normally introduce this in quantum theory by turning classical variables which commute, into quantum operators which do not. The classic example is a system with position and momentum, x and p. We know that xp-px=[x,p]=0.
x and p here are just numbers with units attached. The order in which they are written does not matter. However, when we make the transition to quantum theory we get xp-px -> x̂ p̂ – p̂x̂ =[x̂,p̂] = i ħ. Order now matters.
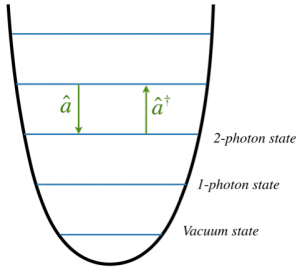
Now if classical light satisfies the simple harmonic oscillator equation we can use the quantum theory of the harmonic oscillator (diagram on right) as our quantum theory of light.
Current Research Topics