A. M. Yao, C. J. Gibson and G.-L. Oppo, “Control of spatially rotating structures in diffractive Kerr cavities”, Opt. Express 27, 031273 (2019).
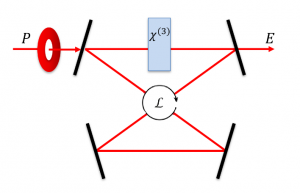In optical cavities, the interplay of a self-focussing nonlinearity, cavity detuning and a spatial coupling, such as diffraction or dispersion instead can result in spontaneous spatial pattern formation due to the Turing instability.
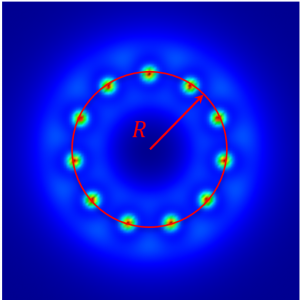If the cavity is pumped by a beam carrying orbital angular momentum (OAM) m, the Turing patterns rotate with an angular velocity of magnitude ω = 2m / R^2 on rings of radii R. For top-hat pumps carrying OAM, concentric rings of patterns each rotating at different angular velocities are formed.
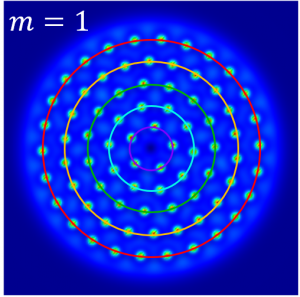Full control over the angular velocity of the pattern in the range -2m / R^2 < ω < 2m / R^2 is obtained by using cylindrical vector beam pumps that consist of orthogonally polarized eigenmodes with equal and opposite OAM.
Using Poincaré beams that consist of orthogonally polarized eigenmodes with different magnitudes of OAM, and assuming good overlap between the eigenmodes, the resultant angular velocity has magnitude ω = (m_L + m_R) / R^2, where m_L, m_R are the OAMs of the eigenmodes.
If there is no, or very little, overlap between the modes then concentric Turing pattern rings, each with angular velocity ω = 2m_L,R / R^2 will result.
This can lead to, for example, concentric, counter-rotating Turing patterns creating an optical peppermill-type structure:
Full control over the speeds of multiple rings has potential applications in particle manipulation and stretching, atom trapping, and circular transport of cold atoms and BEC wavepackets.