Light beams that can propagate without a significant change to their spatial profile are of interest for modern optical technologies and high-power laser systems. Self-trapped light filaments, or spatial solitons, are formed when their spreading due to linear diffraction is carefully balanced by a self-focusing (Kerr) nonlinearity that causes the beam to narrow. Because of their potential to carry an increased information content, there has been significant interest in the formation of spatial solitons carrying orbital angular momentum (OAM).
F. Bouchard, H. Larocque, A. M. Yao, C. Travis, I. De Leon, A. Rubano, E. Karimi, G.-L. Oppo and R. W. Boyd, “Polarization shaping for control of nonlinear propagation”, Phys. Rev. Lett. 117, 233903 (2016).
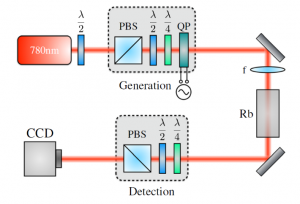Working in collaboration with Dr. Robert Boyd’s group at the University of Ottowa, we study the nonlinear optical propagation of two different classes of light beams carrying OAM and with space-varying polarization—radially symmetric vector beams and Poincaré beams with lemon and star topologies—in a rubidium vapor cell.
Unlike Laguerre-Gauss and other types of beams that quickly experience instabilities, we observe that their propagation is not marked by beam breakup while still exhibiting traits such as nonlinear confinement and self-focusing. Our results suggest that, by tailoring the spatial structure of the polarization, the effects of nonlinear propagation can be effectively controlled. These findings provide a novel approach to transport high-power light beams in nonlinear media with controllable distortions to their spatial structure and polarization properties.
C. J. Gibson, P. Bevington, G.-L. Oppo and A. M. Yao, “Control of polarization rotation in nonlinear propagation of fully structured light“, Phys. Rev. A, 97, 033832 (2018).
Knowing how the spatial polarization distribution of a beam is affected by propagation is of importance in many applications that depend on the state of polarization. We have analytically calculated the polarization rotation of fully structured light beams during linear propagation and shown that the observed rotation is due entirely to the difference in Gouy phase between the two eigenmodes comprising the FSL beams. This allows the exact polarization state at a particular propagation distance to be controlled simply by choosing the eigenmodes of the FSL beam and the beam size.
We have shown that polarization rotation is also affected by propagation through a self-focusing (Kerr) nonlinear medium and that this can be controlled by changing the eigenmodes of the superposition and physical parameters such as the beam size, the amount of Kerr nonlinearity, and the input power.
By biasing cylindrical vector beams to have elliptical polarization, we can vary the polarization state from radial through spiral to azimuthal using nonlinear propagation:
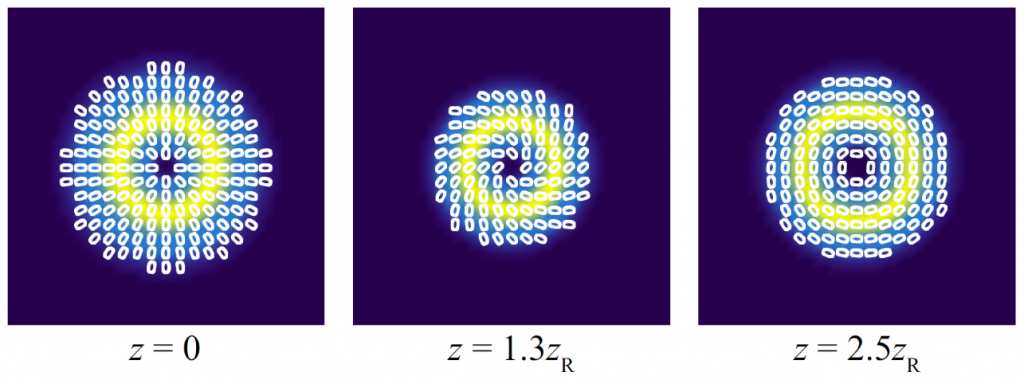
The ability to control both the intensity and polarization of FSL beams may provide a useful method for applications in micromachining and microscopy.