Scalar and Vectorial Kerr-resonators
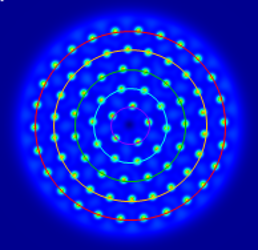
Research on emergent behaviour of new structures in Kerr resonators started in the CNQO group in the early 1990s. These nonlinear structures include Turing patterns and cavity solitons were discovered at Strathclyde by A. J. Scroggie and W. J. Firth in 1994. Figure 3 shows a typical Turing hexagonal pattern in the transverse output of a scalar (single field) Kerr resonator.
|
|
|
|
|
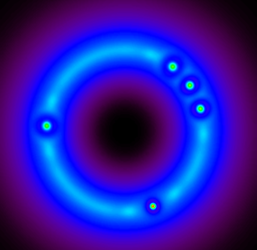
| Fig. 3: Hexagonal Turing pattern | Fig. 4: Rotating rings | Movie 1: Rotating Patterns | Fig. 5: Rotating cavity solitons |
If the input pump is an optical beam with orbital angular momentum (corkscrew phase), the intensity peaks of the Turing pattern re-arrange themselves on concentric circles that rotates with angular velocity proportional to the orbital angular momentum and inversely proportional to the square of the radius of the circles (Figure 4). In Figure 5 we see transverse cavity solitons in the Kerr resonator rotating at the same angular velocity of the pattern while in the Movie 1 we see the rotation of azimuthal Turing patterns in vectorial Kerr resonator pumped by two beams of OPPOsite circular polarisation and optical angular momentum as well as different radii.
Similar effects have been observed in cavities filled with cold atoms where the Kerr nonlinearity has been replaced by an opto-mechanical one leading to atomic rotational transfer.
Recent References
A. M. Yao, C. J. Gibson and G.-L. Oppo, “Control of spatially rotating structures in diffractive Kerr cavities”, Opt. Express 27, 031273 (2019).
G. Baio, G. R. M. Robb, A. M. Yao and G.-L. Oppo, “Optomechanical transport of cold atoms induced by structured light”, Phys. Rev. Res. 2, 023126 (2020).