A. Di Carli, C. D. Colquhoun, G. Henderson, S. Flannigan, G.-L. Oppo, A. J. Daley, S. Kuhr and E. Haller, “Excitation modes of bright matter-wave solitons”, Phys. Rev. Lett 123, 123602 (2019).

Working in collaboration with an experimental team from the Experimental Quantum Optics and Photonics Group, we study the excitation modes of bright matter-wave solitons in a quasi-one-dimensional geometry. These solitons are created by quenching the interactions of a Bose-Einstein condensate of caesium atoms from repulsive to attractive interactions, whilst at the same time introducing a rapid reduction of the longitudinal confinement. A deliberate mismatch of quench parameters allows for the excitation of breathing modes of the emerging soliton and for the determination of its breathing frequency as a function of atom number and confinement. The frequency of the breathing dynamics are demonstrated to show good agreement between experimental results and numerical simulations of the one-dimensional Gross-Pitaevskii equation.

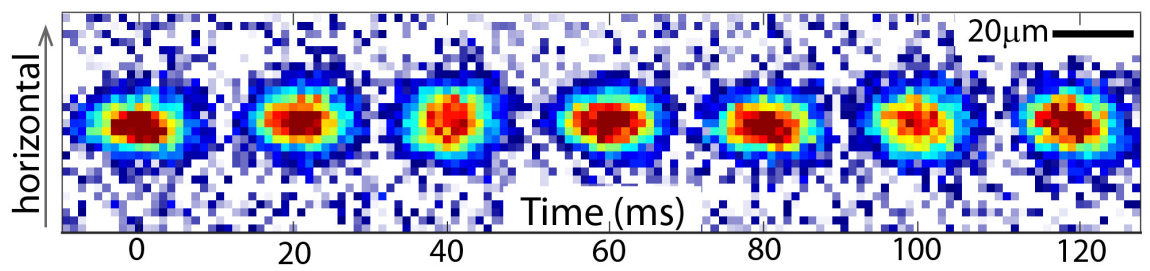
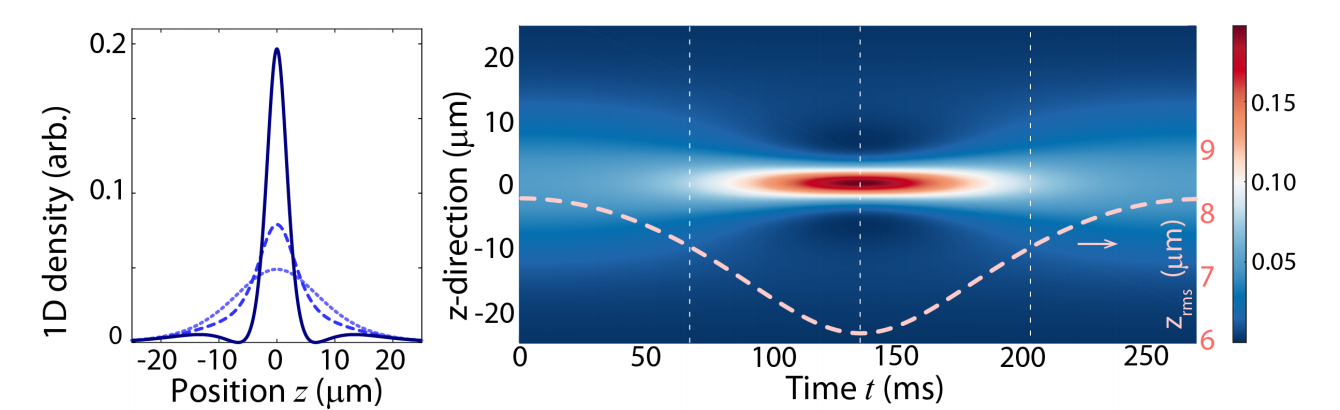
In addition to the breathing motion, we observe signatures of higher-order solitons and the splitting of the wave packet after the quench with a sufficiently wide initial soliton. Our experimental results are again compared to analytical predictions and to numerical simulations of the one-dimensional Gross-Pitaevskii equation, where good agreement is again obtained for second- and third-order solitons. Results for the characteristic behaviour of second (left hand side) and third-order (right hand side) solitons are shown below from numerical simulations.

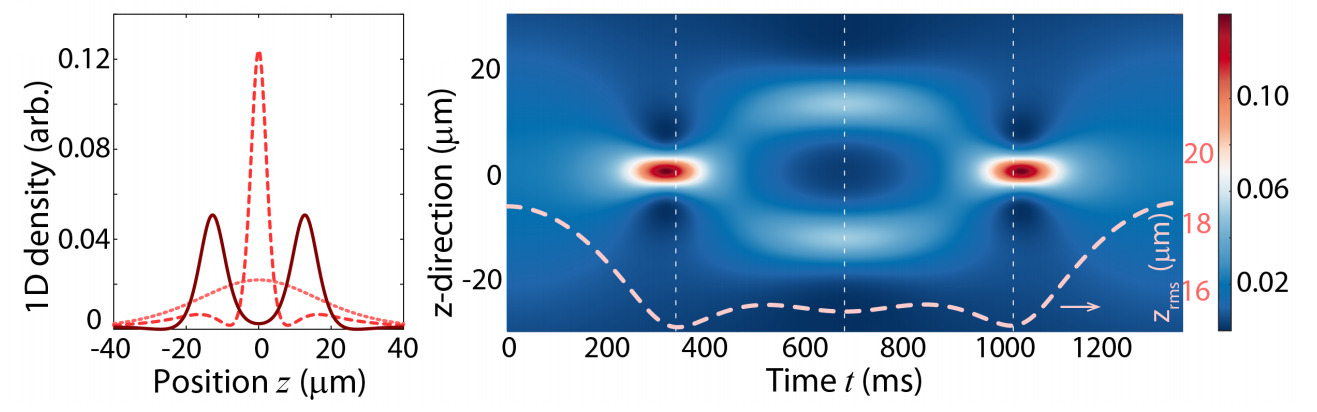Numerical simulations of the second order soliton breathing process. Right hand plot of the time evolution of z-direction density with overlaid root-mean square width of soliton. Vertical lines correspond to times of one-dimensional density cuts (left hand side).	Numerical simulations of the third order soliton breathing process. Right hand plot of the time evolution of z-direction density with overlaid root-mean square width of soliton. Vertical lines correspond to times of one-dimensional density cuts (left hand side).