Quantum Entanglement in Orbital Angular Momentum
We live in an information-based society where ensuring the security of our communications is of critical significance. New protocols in quantum information science based on the orbital angular momentum [3] states of photons have the potential to boost data rates in optical communication. Photons that are entangled in their OAM can be reliably produced using a process known as spontaneous parametric down-conversion (SPDC) and we have demonstrated the quantum nature of these photons and their potential for applications in quantum information protocols [1, 5-7].
The down-converted photons consist of a superposition of OAM modes, where the number of modes – the spiral bandwidth – is related to the degree of entanglement. They can be expressed as a superposition of Laguerre–Gauss (LG) modes [Torres 2003] and for short crystals and/or perfect phase matching we have calculated the down-converted state for any Laguerre-Gaussian pump [2, 3]. These modes have important implications for quantum information science because they reside in an infinite-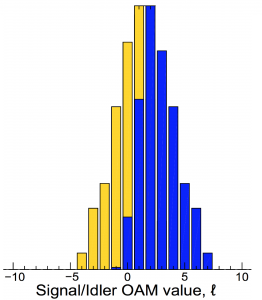 dimensional state space, thus allowing the possibility of impressing large amounts of information onto a single photon. In addition to increasing the information capacity, entangling photons in higher dimensional states can also help reduce the detrimental effect of noise. We can the control the spiral bandwidth (SB), and hence the quantum state of the generated photons, by manipulating the spatial profile of the pump beam or changing the ratio between the width of the pump and the width of the down-converted modes.
dimensional state space, thus allowing the possibility of impressing large amounts of information onto a single photon. In addition to increasing the information capacity, entangling photons in higher dimensional states can also help reduce the detrimental effect of noise. We can the control the spiral bandwidth (SB), and hence the quantum state of the generated photons, by manipulating the spatial profile of the pump beam or changing the ratio between the width of the pump and the width of the down-converted modes.
Photons carrying OAM have been used to demonstrate the Einstein, Podolosky, Rosen (EPR) paradox [Einstein 1935, Leach 2010] and the Heisenberg Uncertainty relation for OAM and its conjugate variable, angular position [Barnett 1990, Jack 2011].
Relevant papers
- J. Leach et al., Phys. Rev. A, 85, 013827 (2012).
- A. M. Yao, New J. Phys., 13, 053048 (2011).
- F. M. Miatto et al., Phys. Rev. A, 83, 033816 (2011).
- A. M. Yao and M. J. Padgett, Adv. Opt. Photon. 3, 161-204 (2011).
- B. Jack et al., Phys. Rev. A 81, 043844 (2010).
- J. Leach, et al., Science 329, 662-665 (2010).
- R. W. Boyd et al., Optics & Photonics News 21, 48 (2010).