High precision sensors have been one of the greatest drivers of fundamental science and technologies. Consider imaging as just one example of this. Science has historically leapt forward in tandem with improvements to imaging techniques. However, the push for better resolutions in imaging devices has seen a sharp increase in the number of pixels used per unit area. With such miniaturisation, each pixel is illuminated with small photon fluxes, down to the detection of single photons. Any further performance improvements is inherently limited by the quantum properties of light. This is the so-called Rayleigh diffraction limit and reflects the same difficulties as the `death march of Moore’s law’ in manufacturing.
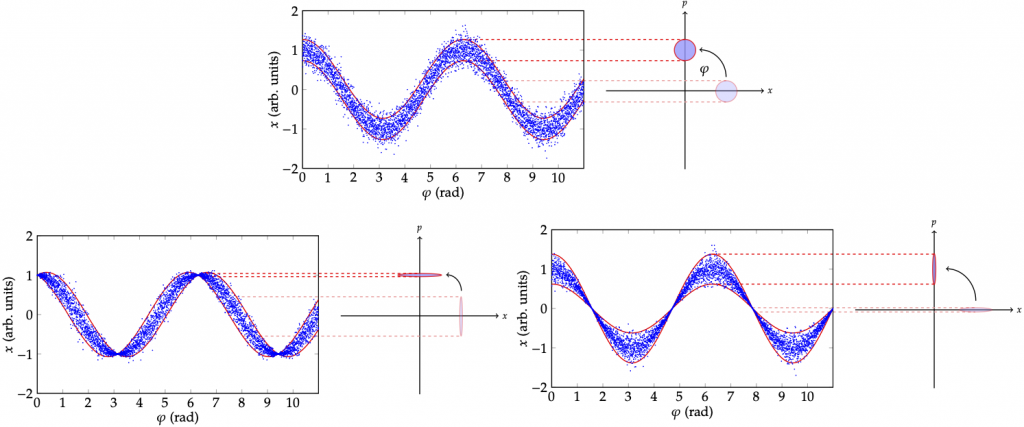
Phase and amplitude squeezed coherent states are important in the estimation of phase or amplitude of optical fields.
Quantum information theory can help define fundamental limits to the precision of measurements, which helps characterise the performance of quantum sensors. The mathematical machinery behind this is quantum estimation theory, which naturally give rise to a rich geometrical view of quantum metrology. It is now understood that the ultimate limit is expressed in terms of the physical resources used in the measurement procedure. But there are still many open questions.
- What are the best probe states to use for robust quantum metrology?
- What is the best strategy to simultaneously estimate non-compatible observables?
- How can fault tolerant schemes help in practical quantum metrology?
At Strathclyde, we work on developing novel theoretical tools that describe the best attainable estimation precisions in general estimation settings.
For example, the Holevo Cramér-Rao bound (HCRB) is a fundamental bound on multi-parameter estimations. With some optimisation theory gymnastics, we recently derived new analytic and numerical solutions for the HCRB. Our numerical approach has a quadratic speedup over SDP solvers, which makes the HCRB more accessible for many applications.
PUBLICATIONS
[1] Quantum metrology of spatial deformation using arrays of classical and quantum light emitters, J S Sidhu and P Kok, Physical Review A 95 (6), 063829 (2017).
[2] Tight bounds on the simultaneous estimation of incompatible parameters, J S Sidhu, Y Ouyang, E T Campbell, P Kok, arXiv preprint arXiv:1912.09218 (2019).
[3] Geometric perspective on quantum parameter estimation, J S Sidhu and P Kok, AVS Quantum Science 2 (1), 014701 (2020).
[4] Tight Bounds on the Simultaneous Estimation of Incompatible Parameters, J S Sidhu, Y Ouyang, E T Campbell, and P Kok, Physical Review X 11, 011028 (2021).