A. Di Carli, G. Henderson, S. Flannigan, C. D. Colquhoun, M. Mitchell , G.-L. Oppo, A. J. Daley, S. Kuhr and E. Haller, “Collisionally inhomogeneous Bose-Einstein condensates with a linear interaction gradient”, Phys. Rev. Lett. 125, 183602 (2020).
Working in collaboration with an experimental team from the Experimental Quantum Optics and Photonics Group, we study the evolution of a collisionally inhomogeneous matter wave in a spatial gradient of the interaction strength. Starting with a Bose-Einstein condensate with weak repulsive interactions in quasi-one-dimensional geometry, we monitor the evolution of a matter wave that simultaneously extends into spatial regions with attractive and repulsive interactions. We observe the formation and the decay of soliton-like density peaks, counter-propagating self-interfering wave packets, and the creation of cascades of solitons.
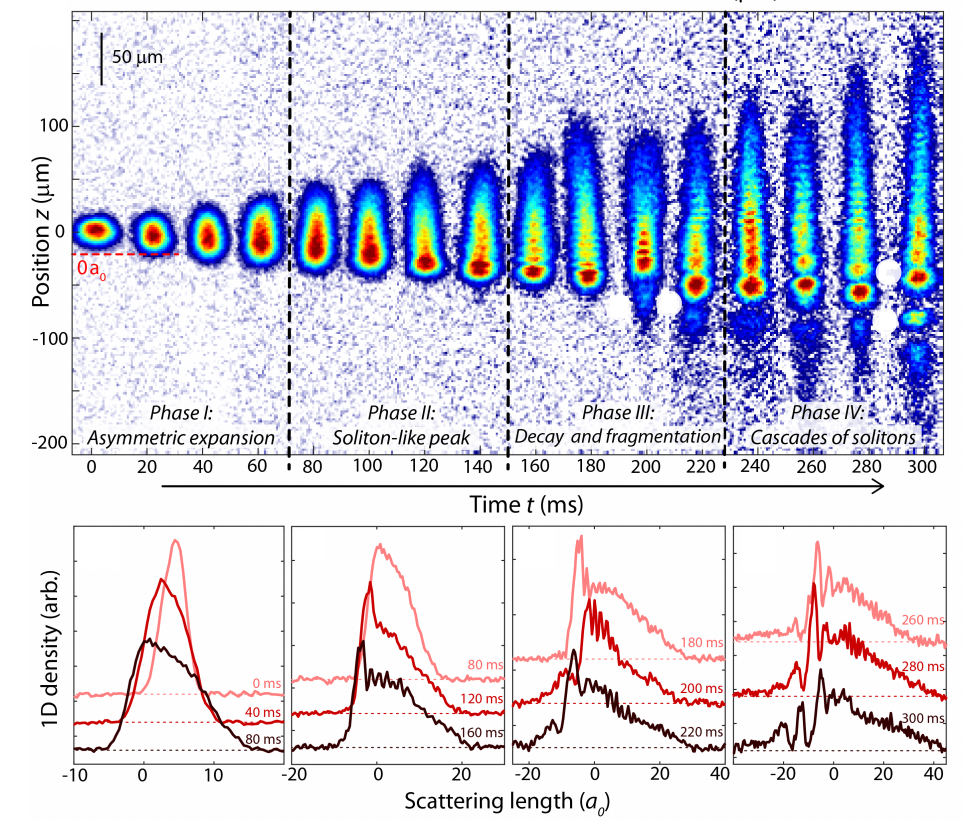
The matter-wave dynamics are well reproduced in numerical simulations based on the nonpolynomial Schroedinger equation (NPSE) with three-body loss, allowing us to better understand the underlying behaviour based on a wavelet transformation. Our analysis provides new understanding of collapse processes for solitons, and opens interesting connections to other nonlinear instabilities.
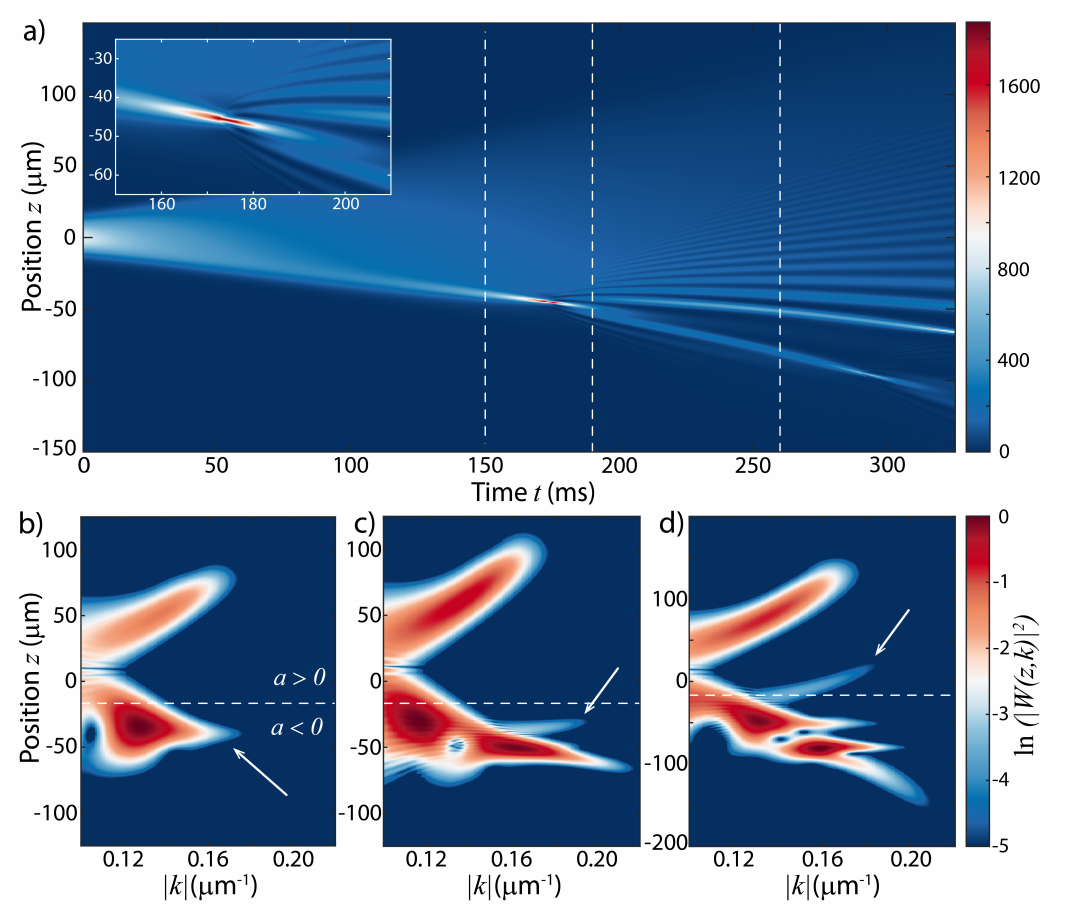
(a) Numerical simulation of the evolution of the density profile using NPSE with three-body loss (1D-density in atoms/µm). Inset: Zoomed region of the growing and then decaying soliton. (b) Wavelet decomposition of the atomic wave function at t = 150 ms (first vertical line in (a)), showing the emerging soliton (white arrow). (c) Wavelet decomposition at t = 190 ms (second vertical line in (a)), after the appearance of the density ripples. The arrow indicates the counter-propagating wave packet. (d) Wavelet decomposition at t = 210 ms (third vertical line in (a)), after the counter-propagating wave packet identified by the arrow penetrates the region of repulsive interactions (a > 0).